0%

Random Forest

发表于 分类于

梳理 Random Forest(随机森林) 算法原理

foreword

  • 随机森林就是通过集成学习的思想将多棵树集成的一种算法，它的基本单元是决策树，而它的本质属于机器学习的一大分支——集成学习（Ensemble Learning）方法。通过组合多棵独立的决策树后根据投票或取均值的方式得到最终预测结果的机器学习方法，往往比单棵树具有更高的准确率和更强的稳定性。随机森林相比于决策树拥有出色的性能主要取决于随机抽取样本和特征和集成算法，前者让它具有更稳定的抗过拟合能力，后者让它有更高的准确率。

Bagging思想

  • Bagging是bootstrap aggregating。思想就是从总体样本当中随机取一部分样本进行训练，通过多次这样的结果，进行投票获取平均值作为结果输出，这就极大可能的避免了不好的样本数据，从而提高准确度。因为有些是不好的样本，相当于噪声，模型学入噪声后会使准确度不高。
  • bagging有以下几种方式增强鲁棒性
    1. 数据样本扰动 （RF采用）
      • 给定初始数据集，可从中产生生不同的数据子集，再利用不同的数据子集训练出不同的个体学习器.数据样本扰动是基于采样法，例如Bagging采用自助法采样，，对很多的常见基学习器，例如决策树，神经网络等，训练样本稍加变动就会导致学习器有显著变化，这些学习器称为‘不稳定基学习器’，但是也有稳定学习器，对于样本扰动，这样的学习器往往不会出现太显著的变化，例如线性学习器，除非特别离群的点，一般的话对拟合直线影响不大；支持向量机，与支持向量关系比较大，其他地方的点对学习器影响不大；朴素贝叶斯，在样本分布相对固定时，样本足够多时样本扰动不足以大幅度改变概率；K近邻学习器，主要与K个邻居有关，而与其他位置的点关系不大，这类学习器称为稳定学习器.对于这类学习器集成，往往需要属性扰动等机制.但是值得一提的是，数据样本扰动会改变样本初始的分布，会人为的引入偏差，也会影响基学习器的性能.
    2. 输入属性扰动 （RF采用）
      • 训练集的输入向量X通常不是一维的，这里我们假设输入数据维度是K维，从而选择不同的子属性集提供了观察数据的不同视角，显然从不同属性子空间训练出来的学习器会有所不同，著名的随机子空算法就依赖于属性扰动，该算法从初始属性集中抽出若干个子集，再基于每个属性子集训练一个基学习器.在包含大量属性的情况下，在属性子空间训练个体学习器不仅能产生多样性大的个体，还会因为属性维数减少提高训练效率，但当数据维数较小或数据的属性都有较大重要性时，不宜使用属性扰动.
    3. 输出表示扰动
      • 此类做法的基本思想是对输出表示进行操纵以增强多样性，可对训练样本的类别标记稍作变动，但要注意尺度，如果变动较大，则会人为引入较大偏差，反而得不偿失.例如二分类到多分类问题，MvM中使用的ECOC法，就是通 过改变输出表示，最后采用投票法决定样本类别.
    4. 算法参数扰动
      • 这个和我们常说的调参比较相似，一个基学习器算法都对应着或多或少的超参数，通过对算法参数的调整，往往能够得到不同性能的学习器，例如设置神经网络的隐层神经元数，决策树的深度，支持向量机的带宽width等等.

随机森林的基本结构

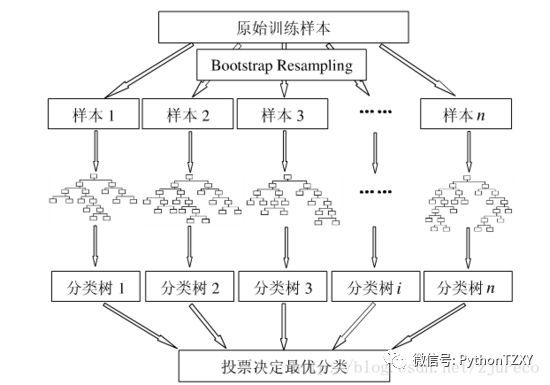
  • rf1.jpeg
  • 常见使用cart作为构建单棵树，对于每一颗子树，输入的数据集和属性都是random的，通过最后的ensemble对结果进行汇总

随机森林如何工作

  • 随机森林的是通过一个个弱的分类器（决策树）最终组成一个强分类器，那么森林中的每棵树是如何生成的呢？

    1. 假设训练集大小为N，采用Bootstrap sample的方法，对每棵树，随机有放回地从训练集中抽取N个训练样本，作为该棵树的训练集；

      • 每棵树的训练集都是不同的，而且里面可能包含重复的训练样本
      • 当通过替换采样绘制当前树的训练集时，大约三分之一的情况被遗漏在样本之外。 随着树木被添加到森林中，该oob（out-of-bag）数据用于获得对分类错误的运行无偏估计。 它还用于获得变量重要性的估计。
        • oob并没有用于构建第k棵树。将每个案例放在第k树的第k树的构造中，以获得分类。 以这种方式，在大约三分之一的树中为每种情况获得测试集分类。 在运行结束时，将j作为每次案例n为oob时获得大多数选票的类。 在所有情况下，j不等于n的真实等级的次数的比例是oob误差估计。 事实证明，这在许多测试中都是公正的。

    2. 假设每个样本的特征维度为M，制定一个常熟m<<M，随机地从M个特征中选取m个特征子集，每次树进行分裂时，从这m个特征中选择最优的

    3. 每棵树都尽最大程度地生长，不进行剪枝（因为每棵树本身虽然可能拟合很好，但是对整体数据集是几乎不可能过拟合的，不需要剪枝提高鲁棒性）
    4. 预测新的样本时，只需要将N棵决策树的分类结果合并输出

错误率

  • 在关于随机森林的原始论文中，显示森林错误率取决于两件事：
    • 森林中任何两棵树之间的相关性。 增加相关性会增加森林错误率。
    • 森林中每棵树的力量(具有低错误率的树是强分类器)。 增加单个树木的强度(分类更精确)会降低森林错误率。

重要性评估

  • 判断每个特征在随机森林中的每颗树上做了多大的贡献，然后取个平均值，最后比一比特征之间的贡献大小。其中关于贡献的计算方式可以是基尼指数或袋外数据错误率。

  • rf2.jpeg

  • rf3.jpeg

  • 附sklearn代码

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    from sklearn.cross_validation import train_test_split
    from sklearn.ensemble import RandomForestClassifier

    x, y = df.iloc[:, 1:].values, df.iloc[:, 0].values
    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.3, random_state = 0)
    feat_labels = df.columns[1:]
    forest = RandomForestClassifier(n_estimators=10000, random_state=0, n_jobs=-1)
    forest.fit(x_train, y_train)
    importances = forest.feature_importances_
    indices = np.argsort(importances)[::-1]
    for f in range(x_train.shape[1]):
        print("%2d) %-*s %f" % (f + 1, 30, feat_labels[indices[f]], importances[indices[f]]))